R6522が持つ2つのタイマーのうちタイマー1は、設定した初期値(Nとする)の間隔でI/OポートBのPB7ピンの信号を反転させる機能を持っています。つまりNの値を変えることで任意の周波数の矩形波を出力できるのです。JR-100ではこれを利用して、PB7にスピーカーを接続していて、任意の音程の音を鳴らすことができます。
さて、R6522のデータシートによると、PB7の反転周期は初回がN+1.5サイクル、2回目以降はN+2サイクルとあります。図の説明ではタイマーが0になるたびに初期値Nがロードされデクリメントを続けるとあるので、一見するとNサイクル周期になるような気がします。それなのになぜなぜN+1.5だったりN+2になったりするのか? これを調べるためにJR-100実機でテストプログラムを作成し検証してみました。
データシートからの推測
まずR6522のデータシートより。
タイマー1は16ビットのカウンタで、上位バイトと下位バイトをそれぞれT1C-Hレジスタ、T1C-Lレジスタに格納しています。またカウンタの初期値を保存するためのラッチも備えていて、同様にT1L-Hレジスタ、T1L-Lレジスタにそれぞれ上位バイトと下位バイトを格納しておきます。
このT1C-Hレジスタにデータを書き込むと同時にT1C-LにT1L-Lのデータがロードされ、タイマーのデクリメントを開始します。
で、この図から分かること:
- 初回のPB7の反転は、Φ2の立ち下がりと同期する(現象1)。
- 2回目以降のPB7の反転は、Φ2の立ち上がりと同期する(現象2)。
- PB7が最初に反転するまでの時間はN+1.5サイクルである(現象3)。
- PB7が次に反転するまでの時間はN+2サイクルである(現象4)。
以下ではこれらの現象をそれぞれ考えていきます。
テストプログラムによる検証
JR-100で以下のプログラムを実行します。
VIA: .EQU 0xc800 T1CL: .EQU 0x04 T1CH: .EQU 0x05 T1LL: .EQU 0x06 T1LH: .EQU 0x07 ACR: .EQU 0x0b .ORG 0x3000 START: LDX VIA LDAB [VIA+ACR] ANDB 0x3F ORAB 0xC0 ; フリーランモード、PB7有効 STAB [VIA+ACR] CLR [VIA+T1LH] STAA [VIA+T1LL] ; AはBASICから渡す。 LDAB 0x00 STAB [VIA+T1CH] ; カウント開始 NOP ; 2サイクル NOP ; 2サイクル NOP ; 2サイクル LDAA [VIA+T1CL] ; 4サイクル STAA [0x3100] RTS
10 POKE 0,0 20 INPUT N 30 A=USR($3000,0,N) 40 PRINT HEX$(PEEK($3100))
マシン語部は、タイマー1をフリーランモード(PB7矩形波出力)に設定し、BASIC部からアキュムレータAに渡された値をタイマー1の初期値とします。NOPを3回挟んだのち、タイマー1の下位バイト(T1C-L)をreadし、0x3100番地に保存します。NOPは2サイクル、LDAA命令のExtendedモードは4サイクルなので、カウントを開始してからちょうど10サイクル目のカウンタ値を求めるプログラムになっています。
BASIC部は、ユーザが入力した数(N)をUSR関数を用いてアキュムレータAに渡し、アドレス0x3000から実行します。その後、アドレス0x3100からデータを読み出し、16進数で表示します。行番号10はキーを押したときのBEEP音を消すためのものですが、その理由は後述します。
これを6802アセンブラとFSKプレイヤーを使ってJR-100に読み込ませ、いろいろなNに対して実行した結果が以下です。
| N | 結果 |
|---|---|
| 12 | 03 |
| 11 | 02 |
| 10 | 01 |
| 9 | 00 |
| 8 | FF |
| 7 | 07 |
| 6 | 05 |
| 5 | 03 |
9カウントしかしかしていない(N=12~9のとき)
Nが12から9のとき、結果はNから9を引いた数になりました。予想では10を引いた数になるはずですがなぜ? ここでタイマー1の別のモードであるワンショットモードの図を見てみます。
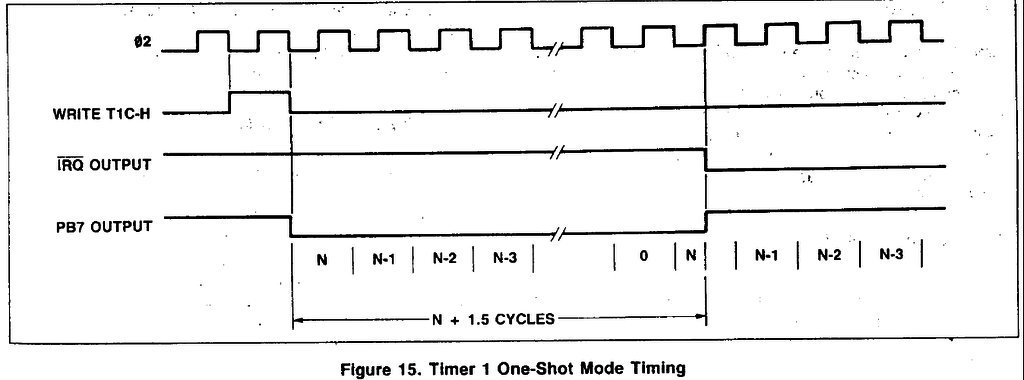
この図から分かること:
- Φ2の立ち下がり時にカウンタ値が1減る。
- Φ2の立ち上がり時にPB7のレベルが反転する。
- カウンタ値が0のときではなく0の次の状態の時にPB7のレベルが反転する。
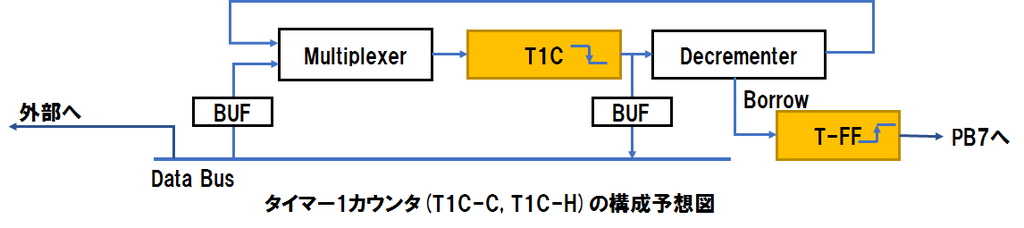
これと現象1、現象2のそれぞれを踏まえると、R6522の内部構成は次の図のようになっていると推測します。
この構成の場合、Φ2クロックの立ち下がり時にDecrementerからの出力がT1Cに記憶されます。また、Φ2の立ち下がりの少し前からΦ2の立ち下がり後間もない間はデータバスにデクリメント前のデータが乗っており、その後デクリメント後のデータに変化します。なおデータバスの値が変化するまでの時間は、MPUが期待するホールド時間以上と仮定します。
(この仮定が間違っていると検討しなおしですが……)
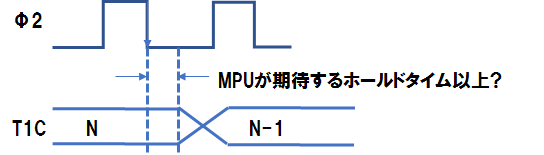
そうすると、MPU側はΦ2クロックの立ち下がり時にデータバス上のデータをreadするので、MPUがロードする値はT1Cのデクリメント前のデータになるはずです。これにより、CPUサイクル数よりもカウンタ値が1少ない理由が説明できました。
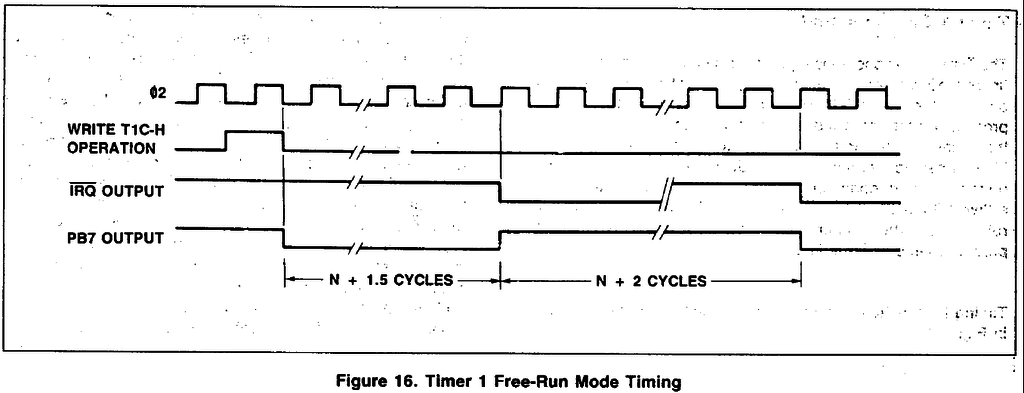
N+2サイクルの理由
次に現象4を考えます。なぜN+2サイクルなのか?
これはテストプログラムの実験結果から分かります。N=9のとき結果が0、N=8のとき結果がFFとなっています。つまりカウンタの状態としてはN, N-1, ..., 0, FF(-1)というN+2個あり、これを繰り返しているからということが分かります。
ところで、PB7に生成される矩形波の周波数をf、クロック周波数をFとすると、次の式が成り立ちます。
f = F / (2 * (N + 2)) [Hz]
N = F / (2 * f) - 2
例えばJR-100(F=890kHz)でラの音(440Hz)を再生するには、T1の初期値Nを以下のようすればよいです。
N = F / (2 * f) - 2 = 890000 / (2 * 440) - 2 ≒ 1009 (0x03F1)
さらに余談ですが、JR-100付属のユーザーズマニュアルの巻末に、ミュージックを再生するためのプログラム、そして夏の扉を演奏するサンプルが載っていることはご存知ですよね:-) そのプログラムではラの音として0x03F6をNとしています。少しずれています。実はJR-100に搭載されている水晶発振子の周波数が14.31818MHzで、これを16分周すると894.88625Hzとなります。この値を上記の式に代入。
N= 894886.25 / (2 * 440) - 2 ≒ 1014.92
そして小数点以下を切り捨てた1014を16進数に変換すると0x03F6となる、ということです。四捨五入して1015(0x03F7)とした方が正確のような……。
N+1.5サイクルの理由
ここまでわかってきたら、現象3の初回のサイクルがN+1.5サイクルである理由は明らかでしょう。通常はΦ2の立ち上がり時にPB7が反転するところが、0.5サイクル遅れてΦ2の立ち下がり時にPB7が反転することが理由です。
Nが7以降の結果が2ずつ減る理由(N=7~5)
これもよく考えれば分かると思います。1周期経過すると、もともとのNの差に加えて先に周期を開始することによるオフセット分があるため、差が拡大するということです。下の表を見れば一目瞭然でしょう。
| 条件 | t | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 |
|---|---|---|---|---|---|---|---|---|---|
| N=5のときのT1Cの値 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | 5 | 4 |
| N=4のときのT1Cの値 | 4 | 3 | 2 | 1 | 0 | -1 | 4 | 3 | 2 |
ロジックアナライザによる検証
これまでの結果をロジックアナライザで取得したデータをもとに検証します。ロジアナはLAP-C(16032)を使います(→参考記事)。
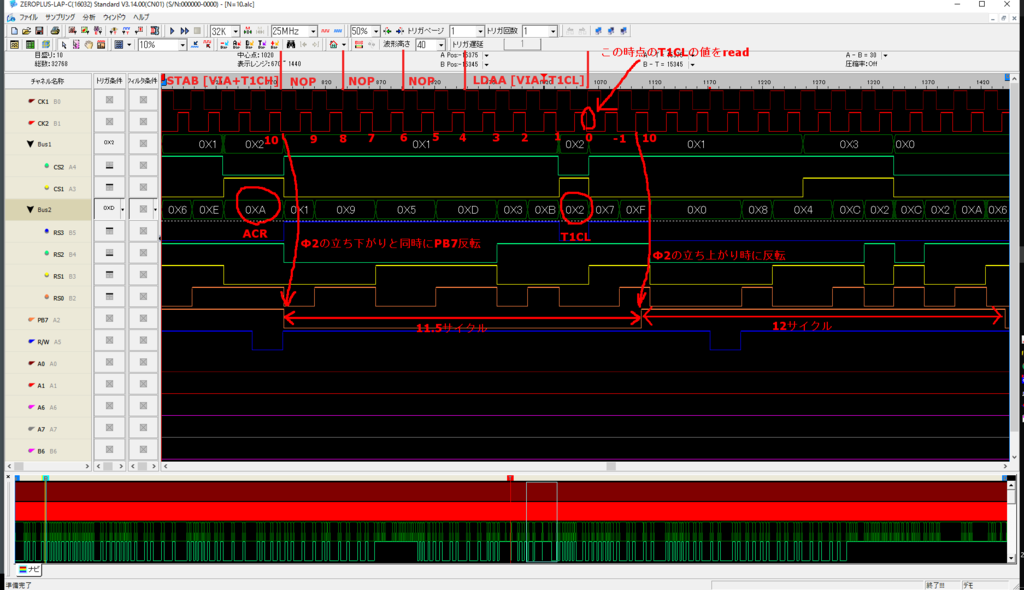
R6522のACRレジスタにアクセスがあったタイミングをトリガーとしてサンプリングします。N=10のときのサンプリング結果に説明を加えました。
ACRレジスタの番号は0x0B(1011)なのですが、RS0~RS3とロジアナ上のピン番号の結線を逆順にしてしまったためアナライザ上は0x0D(1101)となっています。
テストプログラムではT1C-Hレジスタ(0x05; ロジアナ上は0x0A)へのwriteとともにカウント開始します。データシートの図と同じように、確かに11.5サイクル(N+1.5)となっています。また2回目の周期は12サイクル(N+2)となっています。データシートは正しかった。
ちなみにテストプログラムのBASIC部の10行目でキー入力時のBEEP音を消しているのは、20行目のINPUT分で数字を入力する際のBEEP音を鳴らすために、BASIC ROM内部でR6522のレジスタ操作が行われてしまい、テストプログラム用に意図したトリガーをかけられない事態を防ぐためのものです。
まとめ
- R6522のタイマー1は初期値Nに対してN+2サイクルでPB7の信号を反転させる。
- ただし初回のみN+1.5サイクルである。
- タイマー1のカウンタ値はN, N-1, ..., 1, 0, -1の順に繰り返す。




コメント